Peephole optimizations in C++ and C#

“Performance gains due to improvements in compiler optimizations will double
the speed of a program every 18 years” © Proebsting’s Law

When we solve equations, we try to simplify them first, e.g. Y = -(5 - X) can be simplified to just Y = X - 5. In modern compilers it’s called “Peephole Optimizations”. Roughly speaking, compilers search for certain patterns and replace them with corresponding simplified expressions. In this blog post I’ll list some of them which I found in LLVM, GCC and .NET Core (CoreCLR) sources.

Let’s start with simple cases:

1
2
3
4

  X * 1          =>  X
 -X * -Y         =>  X * Y
-(X - Y)         =>  Y - X
  X * Z - Y * Z  =>  Z * (X - Y)

and check the 4th one in C++ and C# compilers:

1
2
3

int Test(int x, int y, int z) {
    return x * z - y * z;       //  =>  z * (x - y)
}

Now let’s take a look at what the compilers output:

1
2
3
4
5

Test(int, int, int):
  mov eax, edi
  sub eax, esi   ; -         
  imul eax, edx  ; *         
  ret
C++ (Clang, GCC, MSVC)
1
2
3
4
5
6

C.Test(Int32, Int32, Int32)  
  mov eax, edx
  imul eax, r9d  ; *
  imul r8d, r9d  ; *
  sub eax, r8d   ; -
  ret
C# (RyuJIT)

All three C++ compilers have just one imul instruction. C# (.NET Core) has two because it has a very limited set of available peephole optimizations and I’ll list some of them later. Be sure to note, the entire InstCombine transformation implementation, where peephole optimizations live, in LLVM takes more than 30K lines of code (+20k LOC in DAGCombiner.cpp). By the way, here is the piece of code in LLVM responsible for the pattern we are inspecting now. GCC has a special DSL which describes all peephole optimizations, and here is the piece of that DSL for our case.

I decided, just for this blog post, to try to implement this optimization for C# in JIT (hold my beer 😛):


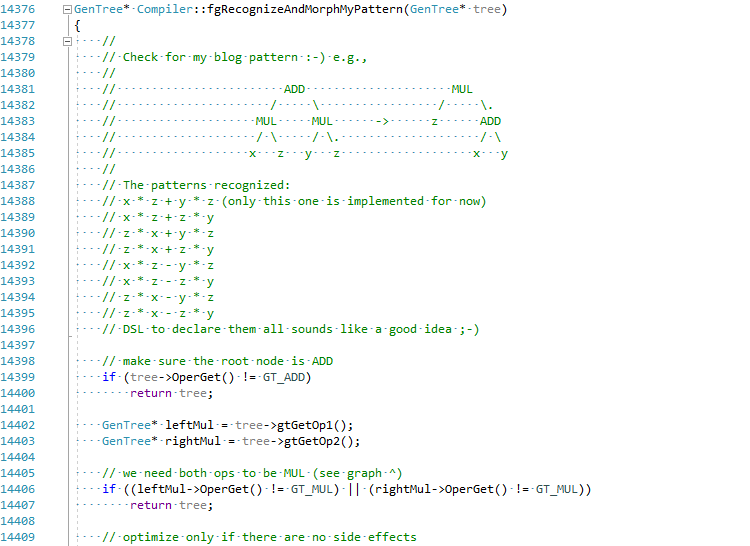
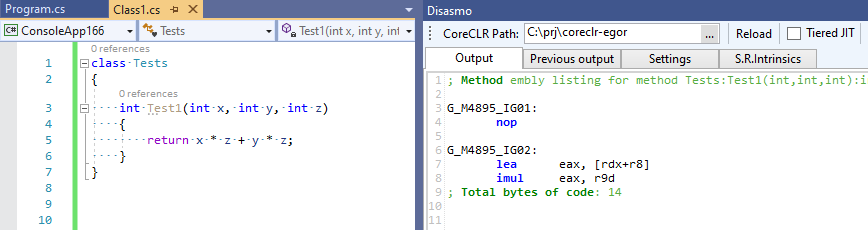
Let’s now test my JIT improvement (see EgorBo/coreclr commit for more details) in VS2019 with Disasmo:

lea + imul instead of imul + imul + add



Let’s go back to C++ and trace the optimization in Clang. We need to ask clang to emit LLVM IR for our C++ code via -emit-llvm -g0 flags (see godbolt.org) and then give it to the LLVM optimizer opt via -O2 -print-before-all -print-after-all flags in order to find out what transformation actually removes that extra multiplication from the -O2 set. (see godbolt.org):

1
2
3
4
5
6
7
8
9
10
11
12
13
14

; *** IR Dump Before Combine redundant instructions ***
define dso_local i32 @_Z5Case1iii(i32, i32, i32) {
  %4 = mul nsw i32 %0, %2
  %5 = mul nsw i32 %1, %2
  %6 = sub nsw i32 %4, %5
  ret i32 %6
}

; *** IR Dump After Combine redundant instructions ***
define dso_local i32 @_Z5Case1iii(i32, i32, i32) {
  %4 = sub i32 %0, %1
  %5 = mul i32 %4, %2
  ret i32 %5
}
It's InstCombine!

So it’s InstCombine indeed, we can even use it as the only optimization for our code for tests via -instcombine flag passed to opt:


Let’s go back to the examples. Look what a cute optimization I found in GCC sources:

1

X == C - X  =>  false if C is odd

And that’s true, e.g.: 4 == 8 - 4. Any odd number for C (C usually means a constant/literal) will always be false for the expression:

Foo2(int x) always returns false. LLVM doesn't have this optimization.

Optimizations vs IEEE754

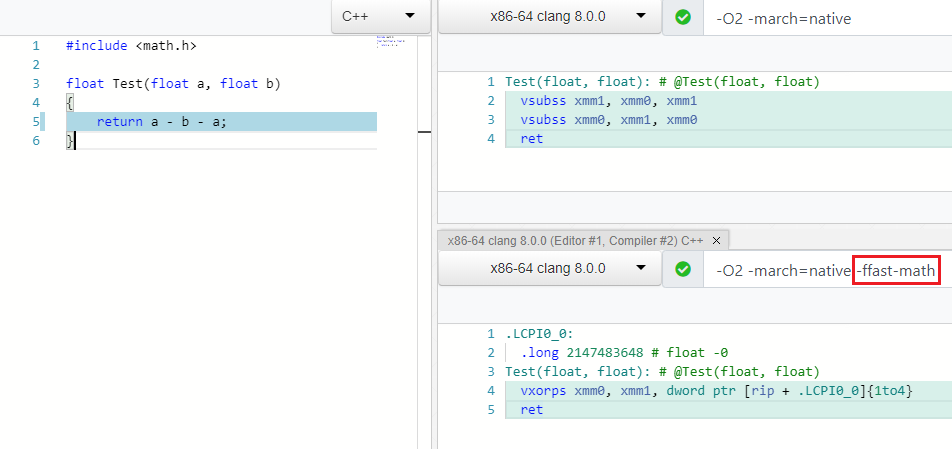
Lots of this type of optimizations work for different data types, e.g. byte, int, unsigned, float. The latter is a bit tricky e.g. you can’t simplify A - B - A to -B for floats/doubles, even (A * B) * C is not equal to A * (B * C) due to the IEEE754 specification. However, C++ compilers have a special flag to let the optimizers be less strict around IEEE754, NaN and other FP corner cases and just apply all of the optimizations - it’s usually called “Fast Math” (-ffast-math for clang and gcc, /fp:fast for MSVC). Btw, here you can find my feature request for .NET Core to introduce the “Fast Math” mode there: dotnet/coreclr#24784).

As you can see, two vsubss were eliminated in the -ffast-math mode:

The C++ optimizers also support math.h functions, e.g.:

1

abs(X) * abs(X)  =>  X * X

The square root is always positive:

1
2

sqrt(X) < Y  => false, if Y is negative.
sqrt(X) < 0  => false

Why should we calculate sqrt(X) if we can just calculate C^2 in compile time instead?:

1

sqrt(X) > C  => X > C * C

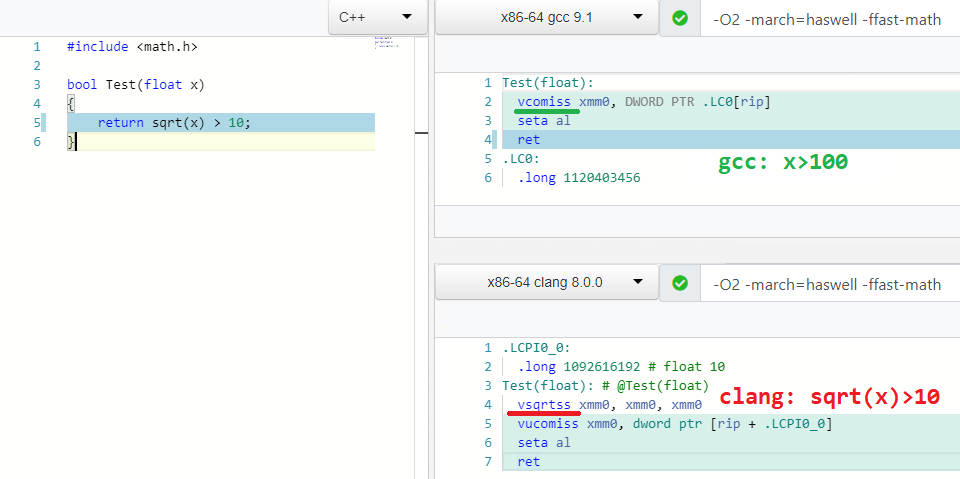
More sqrt optimizations:

1
2
3
4

sqrt(X) == sqrt(Y)  => X == Y
sqrt(X) * sqrt(X)   => X
sqrt(X) * sqrt(Y)   => sqrt(X * Y)
logN(sqrt(X))       => 0.5 * logN(X)

or exp:

1

exp(X) * exp(Y)  => exp(X + Y)

And my favorite one:

1

sin(X) / cos(X)  => tan(X)

There are lots of boring bit/bool patterns:

1
2
3
4
5
6
7
8

((a ^ b) | a) -> (a | b)
(a & ~b) | (a ^ b)  -->  a ^ b
((a ^ b) | a) -> (a | b)
(X & ~Y) |^+ (~X & Y) -> X ^ Y
A - (A & B) into ~B & A
X <= Y - 1 equals to X < Y
A < B || A >= B -> true
... hundreds of them ...

Machine-dependent optimizations

Some operations may be faster or slower on different CPUs, e.g.:

1

X / 2  =>  X * 0.5

mulss/mulsd usually have better both latency and throughput than divss/divsd for example, here is the spec for my Intel Haswell CPU:

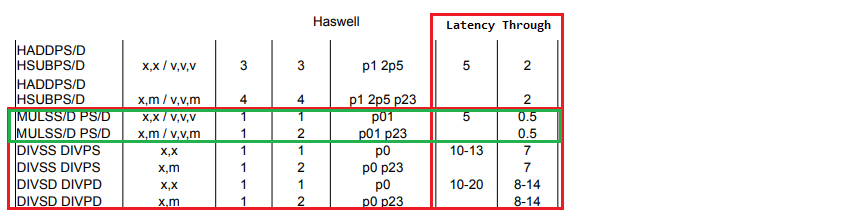
We can replace / C with * 1/C even in the non-“Fast Math” mode if C is a power of two. Btw, here is my PR for .NET Core for this optimization: dotnet/coreclr#24584.

The same rationale for:

1

X * 2  =>  X + X

test is better than cmp (see my PR dotnet/coreclr#25458 for more details):

1
2
3
4

X >= 1  =>  X > 0
X < 1   =>  X <= 0
X <= -1 =>  X >= 0
X > -1  =>  X >= 0

And what do you think about these ones?:

1
2
3
4

pow(X, 0.5)   =>  sqrt(x)
pow(X, 0.25)  =>  sqrt(sqrt(X))
pow(X, 2)     =>  X * X     ; 1 mul
pow(X, 3)     =>  X * X * X ; 2 mul


How many mul are needed to perform pow(X, 4) or X * X * X * X?

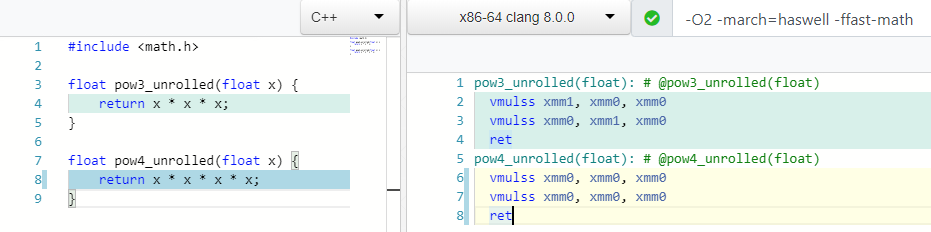
Just 2! Just like for pow(X, 3) and unlike pow(X, 3) we don’t even use the xmm1 register.


Modern CPUs support a special FMA instruction to perform mul and add in just one step without an intermediate rounding operation for mul:

1

X * Y + Z  =>  fmadd(X, Y, Z)


Sometimes compilers are able to replace entire algorithms with just one CPU instruction, e.g.:

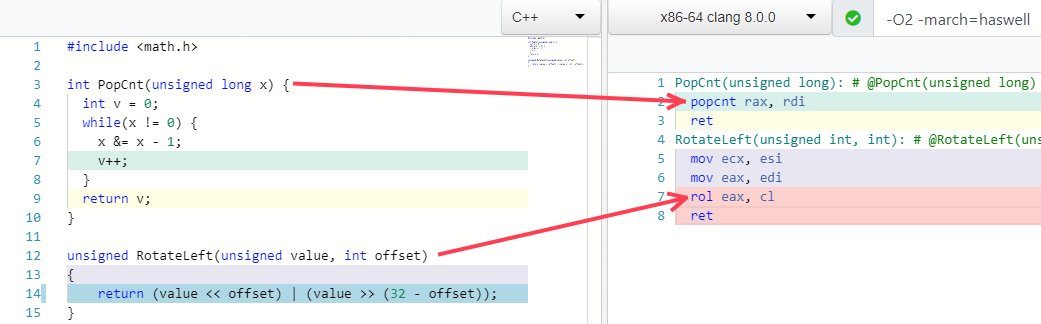
Traps for optimizations

We can’t just find patterns & optimize them:

  • There is a risk to break some code: there are always corner-cases, hidden side-effects. LLVM’s bugzilla contains lots of InstCombine bugs.
  • An expression or its parts we want to simplify might be used somewhere else.

I borrowed a nice example for the second issue from “Future Directions for Optimizing Compilers” article.
Imagine we have a function:

1
2
3
4
5

int Foo1(int a, int b) {
   int na = -a;
   int nb = -b;
   return na + nb;
}

We need to perform 3 operations here: 0 - a, 0 - b, и na + nb. LLVM simplifies it to just two operations: return -(a + b) - what a smart move, here is the IR:

1
2
3
4
5

define dso_local i32 @_Z4Foo1ii(i32, i32) {
  %3 = add i32 %0, %1 ; a + b
  %4 = sub i32 0, %3  ; 0 - %3
  ret i32 %4
}

Now imagine that we need to store values of na and nb in some global variables, e.g. x and y:

1
2
3
4
5
6
7
8
9

int x, y;

int Foo2(int a, int b) {
   int na = -a;
   int nb = -b;
   x = na;
   y = nb;
   return na + nb;
}

The optimizer still recognizes the pattern and simplifies it by removing redundant (from its point of view) 0 - a and 0 - b operations. But we do need them! We save them to the global variables! Thus, it leads to this:

1
2
3
4
5
6
7
8
9

define dso_local i32 @_Z4Foo2ii(i32, i32) {
  %3 = sub nsw i32 0, %0                    ; 0 - a 
  %4 = sub nsw i32 0, %1                    ; 0 - b
  store i32 %3, i32* @x, align 4, !tbaa !2  
  store i32 %4, i32* @y, align 4, !tbaa !2
  %5 = add i32 %0, %1                       ; a + b
  %6 = sub i32 0, %5                        ; 0 - %5
  ret i32 %6
}

4 math operations instead of 3! The optimizer has just made our code a bit slower. Now let’s see what C# RuyJIT generates for this case:

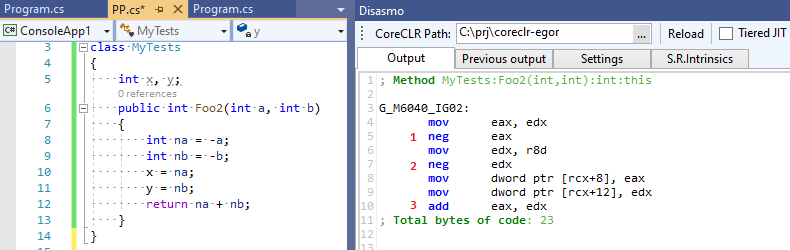
RuyJIT doesn’t have this optimization so the code contains only 3 operations :-) C# is faster than C++! :p

Do we really need these optimizations?

Well, you never know what the final code will look like after inlining, constant folding, copy propagation, CSE, etc.
Also, both LLVM IR and .NET IL are not tied to a specific programming language and can’t rely on quality of the IR it generates. And you can just run your app/lib with InstCombine pass on and off to measure the performance impact.

What about C#?

As I said earlier, peephole optimizations are very limited in C# at the moment. However, when I say “C#” I mean the most popular C# runtime - CoreCLR with RuyJIT. But there are more, including those, using LLVM as a backend: Mono (see my tweet), Unity Burst and LILLC - these runtimes basically use exactly the same optimizations as clang does. Unity guys are even considering replacing C++ with C# in their internal parts. By the way, since .NET 5 will include Mono as an optional built-in runtime - you will be able to use LLVM power for such cases.

Back to CoreCLR - here are the peephole optimizations I managed to find in the morph.cpp comments (I am sure there are more):

1
2
3
4
5
6
7
8
9
10

*(&X)  =>  X
X % 1  => 0
X / 1  =>  X
X % Y  => X - (X / Y) * Y  // arm
X ^ -1  =>  ~x
X >= 1  =>  X > 0 
X <  1  =>  X <= 0
X + С1 == C2  =>  X == C2 - C1
((X + C1) + C2)  =>  (X + (C1 + C2))
((X + C1) + (Y + C2))  =>  ((X + Y) + (C1 + C2))

There are also some in lowering.cpp (machine-dependent ones) but in general RyuJIT obviously loses to С++ compilers here. RyuJIT just focuses more on different things and has a lot of requirements. The main one is - it should compile fast! it’s called JIT after all. And it does it very well (unlike the C++ compilers - see “Modern” C++ Lamentations). It’s also more important to de-virtualize calls, optimize out boxings, heap allocations (e.g. Object Stack Allocation). However, since RyuJIT is now supporting tiers, who knows maybe there will be a place for peephole optimizations in future in the tier1 or even a separate tier2 ;-). Maybe with some sort of DSL to declare them, just read this article where Prathamesh Kulkarni managed to declare an optimization for GCC in just a few lines of DSL:

1
2
3
4
5

(simplify
 (plus (mult (SIN @0) (SIN @0))
       (mult (COS @0) (COS @0)))
 (if (flag_unsafe_math_optimizations)
  { build_one_cst (TREE_TYPE (@0)); }))

for the following pattern:

1

cos^2(X) + sin^2(X) equals to 1